Das Lenz Dreieck: Unterschied zwischen den Versionen
| (25 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
Das Pascalsche Dreieck ist eine Form der grafischen Darstellung der Binomialkoeffizienten, die auch eine einfache Berechnung dieser erlaubt. Sie sind im Dreieck derart angeordnet, dass jeder Eintrag die Summe der zwei darüberstehenden Einträge ist. | Das Pascalsche Dreieck ist eine Form der grafischen Darstellung der Binomialkoeffizienten, die auch eine einfache Berechnung dieser erlaubt. Sie sind im Dreieck derart angeordnet, dass jeder Eintrag die Summe der zwei darüberstehenden Einträge ist. | ||
| − | + | [[Datei:PascalTriangleAnimated-2.gif|zentriert|Das Pascalsche Dreieck]] | |
| Zeile 19: | Zeile 19: | ||
Die Fibonacci-Folge ist die unendliche Folge natürlicher Zahlen, die (ursprünglich) mit zweimal der Zahl 1 beginnt oder (häufig, in moderner Schreibweise) zusätzlich mit einer führenden Zahl 0 versehen ist. Im Anschluss ergibt jeweils die Summe zweier aufeinanderfolgender Zahlen die unmittelbar danach folgende Zahl: | Die Fibonacci-Folge ist die unendliche Folge natürlicher Zahlen, die (ursprünglich) mit zweimal der Zahl 1 beginnt oder (häufig, in moderner Schreibweise) zusätzlich mit einer führenden Zahl 0 versehen ist. Im Anschluss ergibt jeweils die Summe zweier aufeinanderfolgender Zahlen die unmittelbar danach folgende Zahl: | ||
| − | [[Datei:Fibonacci Folge.png|mini| | + | [[Datei:Fibonacci Folge.png|mini|zentriert]] |
| − | [[Datei:Goldene Spirale.png|mini| | + | [[Datei:Goldene Spirale.png|mini|zentriert|Goldene Spirale Fibonacci-Folge]] |
| + | '''Jetzt zu der Idee des Lenz Dreiecks:''' | ||
| + | ---------------------------------------------------- | ||
| + | Das Lenz Dreieck ist eine Form der grafischen Darstellung des exponentiellen Wachstums, welches auch eine einfache Berechnung dessen erlaubt. Im Gegensatz zum Pascalschen Dreieck, wächst das Lenz Dreieck von innen nach außen. Jeder äußere Eintrag ist die Summe der zwei innenliegenden Zahlen an den Dreiecks-Enden. Das System funktioniert mit 3 beliebigen Start-Zahlen. Die Summe der 3 Zahlen des äußeren Dreiecks ist die Verdopplung der Summe der 3 Enden des inneren Dreiecks. | ||
| + | [[Datei:Lenz-Dreieck-01.png|rahmenlos|zentirert]] | ||
| + | |||
| + | [[Datei:Lenz-Dreieck-02.png|rahmenlos|zentirert]] | ||
| + | |||
| + | [[Datei:Lenz-Dreieck-03.png|rahmenlos|zentirert]] | ||
| − | |||
| − | |||
1. Man nehme 3 zufällige Zahlen | 1. Man nehme 3 zufällige Zahlen | ||
| Zeile 34: | Zeile 40: | ||
3. An jede Ecke eine Zahl schreiben | 3. An jede Ecke eine Zahl schreiben | ||
| + | |||
| + | => Die Addition der zueinanderliegenden zwei Zahlen des Dreiecks, ergeben die nächste Zahl des außenliegenden Dreiecks. | ||
| + | |||
| + | => Die Summe der Zahlen des nächsten Dreiecks, ergibt die Multiplikation der Summe des Inneren Dreiecks (x2). | ||
| + | |||
| + | ------------------------------------------------------ | ||
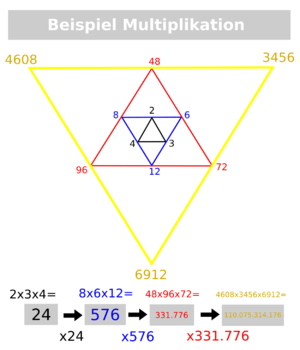
| + | => Es gibt allerdings auch die Möglichkeit, die drei Zahlen einer Dreiecksebene zu multiplizieren (alle beliebigen 3 Zahlen, außer 0 oder 1). Damit potenziert man die Ebenen. | ||
| + | |||
| + | [[Datei:Lenz-Dreieck-Multi-01.png|rahmenlos|zentriert]] | ||
| + | |||
| + | |||
| + | |||
| + | [[Datei:Lenz-Dreieck-Multi-02.png|rahmenlos|zentriert]] | ||
| + | |||
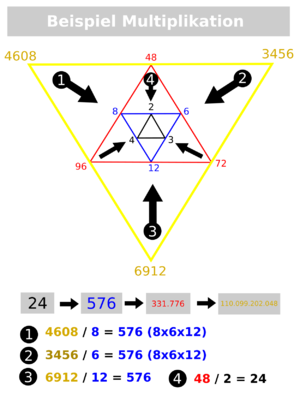
| + | => Dividiert man eine "äußere Dreieckszahl" durch die zu ihr innenliegenden (siehe schwarzer Pfeil), dann erhält man das Ergebnis der Multiplikation der drei innenliegenden Zahlen des kleineren Dreiecks. | ||
| + | |||
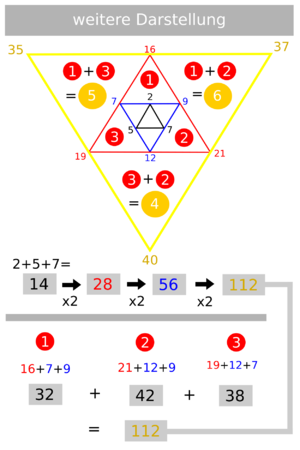
| + | => Selbiges gilt für die Dreiecke bei denen man die Dreieckssumme addiert, wenn man die äußere Zahl mit der innenliegenden subtrahiert. | ||
| + | |||
| + | [[Datei:Lenz-Dreieck-weitere-Bsp-01.png|rahmenlos|zentriert]] | ||
Aktuelle Version vom 15. März 2021, 21:38 Uhr
Das Lenz Dreieck:
Hier bitte ich um die Mithilfe von Mathematikern zur Bewertung der folgenden Entdeckung.
Vorwort:
In der Mathematik gibt es viele Rätsel, Muster und Formen welche sich grundlegend in Zahlen finden und ausdrücken lassen. Das Pascalsche Dreieck oder die Fibonacci-Folge seien als Beispiel genannt.
Beispiel Pascalsches Dreieck:
Das Pascalsche Dreieck ist eine Form der grafischen Darstellung der Binomialkoeffizienten, die auch eine einfache Berechnung dieser erlaubt. Sie sind im Dreieck derart angeordnet, dass jeder Eintrag die Summe der zwei darüberstehenden Einträge ist.
Beispiel Fibonacci-Folge:
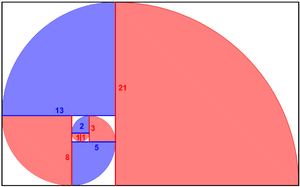
Die Fibonacci-Folge ist die unendliche Folge natürlicher Zahlen, die (ursprünglich) mit zweimal der Zahl 1 beginnt oder (häufig, in moderner Schreibweise) zusätzlich mit einer führenden Zahl 0 versehen ist. Im Anschluss ergibt jeweils die Summe zweier aufeinanderfolgender Zahlen die unmittelbar danach folgende Zahl:
Jetzt zu der Idee des Lenz Dreiecks:
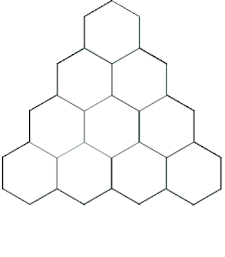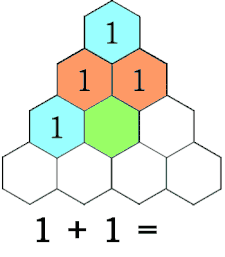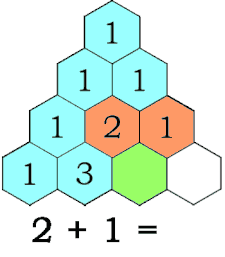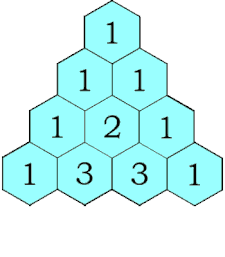
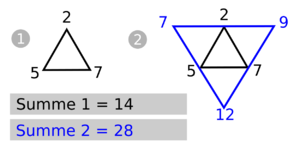
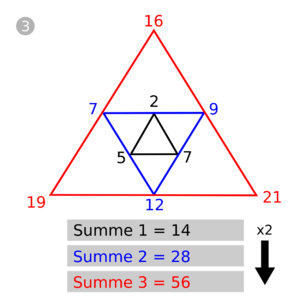
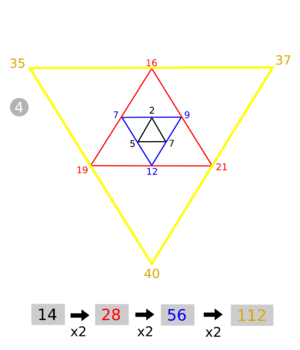
Das Lenz Dreieck ist eine Form der grafischen Darstellung des exponentiellen Wachstums, welches auch eine einfache Berechnung dessen erlaubt. Im Gegensatz zum Pascalschen Dreieck, wächst das Lenz Dreieck von innen nach außen. Jeder äußere Eintrag ist die Summe der zwei innenliegenden Zahlen an den Dreiecks-Enden. Das System funktioniert mit 3 beliebigen Start-Zahlen. Die Summe der 3 Zahlen des äußeren Dreiecks ist die Verdopplung der Summe der 3 Enden des inneren Dreiecks.
1. Man nehme 3 zufällige Zahlen
2. Man zeichnet ein Dreieck
3. An jede Ecke eine Zahl schreiben
=> Die Addition der zueinanderliegenden zwei Zahlen des Dreiecks, ergeben die nächste Zahl des außenliegenden Dreiecks.
=> Die Summe der Zahlen des nächsten Dreiecks, ergibt die Multiplikation der Summe des Inneren Dreiecks (x2).
=> Es gibt allerdings auch die Möglichkeit, die drei Zahlen einer Dreiecksebene zu multiplizieren (alle beliebigen 3 Zahlen, außer 0 oder 1). Damit potenziert man die Ebenen.
=> Dividiert man eine "äußere Dreieckszahl" durch die zu ihr innenliegenden (siehe schwarzer Pfeil), dann erhält man das Ergebnis der Multiplikation der drei innenliegenden Zahlen des kleineren Dreiecks.
=> Selbiges gilt für die Dreiecke bei denen man die Dreieckssumme addiert, wenn man die äußere Zahl mit der innenliegenden subtrahiert.